LIGO R&D
Read more about some of the U.S. National Science Foundation Laser Interferometer Gravitational-wave Observatory's (NSF LIGO) most interesting Research and Development programs
- Optomechanics Research
- Development of Squeezed Light Sources to Improve Advanced LIGO's Sensitivity
- Parametric Instabilities
- Thermal Noise Experiment
- Einstein 1905 versus Einstein 2015
- Crackling Noise in Gravitational Wave Detectors
Optomechanics Research
It has been known since Maxwell first wrote the classical equations of electromagnetism, and indeed earlier suggested by Kepler, that light has momentum and as such will impart momentum when reflected off of a surface. This so-called radiation pressure is responsible for the coupling between the EM field in an optical cavity and the mechanical response of its mirrors. This is one main focus of optomechanics research.
Things become more complicated when we consider the quantum nature of light, which can be thought of as individual photons reflecting from the cavity mirrors at random times. Due to the statistical nature of this process, the fluctuating radiation pressure from the photons will result in fluctuations in the positions of the mirrors. This quantum radiation pressure noise (RPN) limits NSF LIGO’s ability to measure accurately the strain of a passing gravitational wave and it cannot be overcome unless we exploit its quantum mechanical origins. One of the ways that we can do this is by using the correlations between RPN imprints on the amplitude and phase quadratures of the output field to get “squeezing”.
Our experiment here at the MIT LIGO laboratory is designed to measure radiation pressure noise, study it, and find the most effective techniques to mitigate it. Our set-up is essentially a small version of the actual LIGO interferometers in that the heart of the experiment is a Michelson-type interferometer with two one-meter long high-finesse cavity arms with suspended mirrors. Radiation pressure noise will register as fluctuations in the arm lengths of the two cavities, which in turn are monitored with photo-detectors at the antisymmetric port of the interferometer. Input laser power is 10 W, resulting in approximately 20 kW of intra-cavity power. The two end mirrors are expected to “feel” the radiation pressure noise weigh 1 gram, which is small compared to the LIGO test-masses, which feel in order to maximize the effect of radiation pressure. The mirror suspensions are built to minimize thermal noise, which is the dominant source of noise that needs to be overcome. The entire experiment occurs under ultra-high vacuum and is isolated from seismic noise through both passive and active seismic isolation techniques.
Although primarily motivated by the need to understand future quantum noise limitations of advanced LIGO, it is important to understand that any significant RPN signal is an observation of a quantum mechanical effect on a macroscopic object!
Development of Squeezed Light Sources to Improve Advanced LIGO's Sensitivity
The sensitivity of Advanced LIGO is so great that even the discrete nature of light yields measurable effects. In fact, quantization imposes the most significant barrier to improving the LIGO’s sensitivity across its entire measurement band. Most easily conceptualized as shot noise arising from variations in photon arrival time and radiation pressure noise due to fluctuations in the number of photons striking the test masses, this quantum noise is more rigorously described by the interaction of quantum vacuum fluctuations, which enter the readout port of the interferometer with the circulating laser light. Variance in the vacuum's phase quadrature is associated with shot noise, which is significant at high frequencies; variance in the vacuum's amplitude quadrature is related to radiation pressure noise and is most important at low frequencies.
The impact of quantum noise can be changed by, for example, altering the input laser power, changing the mass of the interferometer optics or modifying the parameters of the signal recycling cavity. However, it may also be targeted directly by operating on incident vacuum fluctuations themselves.
The variances in orthogonal quadratures of a vacuum state are governed by a Heisenberg-like-inequality. Exploiting the techniques of nonlinear optics, one can reduce the variance in one quadrature, mitigating the corresponding noise term at the expense of increased variance in the orthogonal quadrature and heightened noise of a different type. The result is called a ‘squeezed vacuum state’, with the act itself known as squeezing. By replacing the naturally occurring vacuum fluctuations entering an interferometer with squeezed vacuum, quantum noise in one quadrature can be reduced.
Squeezing was first demonstrated in 1985 by Slusher et al. At that time, less than 1 dB of noise reduction was achieved at sideband frequencies greater than 400 MHz. Modern squeezers based on degenerate optical parametrical oscillators offer noise reductions of more than 10 dB at frequencies as low as 10 Hz, covering the entire (ground-based) gravitational-wave band. Such devices have been employed at the GEO600 and LIGO Hanford sites, reducing high-frequency shot noise by more than 2 dB and demonstrating that the technique is compatible with long-baseline interferometry.
In these demonstrations, the commensurate increase in low-frequency radiation pressure noise did not affect interferometer performance as it was masked by other effects. In the Advanced LIGO instrument, such effects have been removed through careful design and it is now necessary to ameliorate quantum noise at all frequencies simultaneously by changing the quadrature which is squeezed as a function of frequency: frequency dependent squeezing. The requisite rotation may be achieved by reflecting a squeezed state off a detuned Fabry-Perot resonator known as a filter cavity. Such cavities are required to have extremely low loss as they must store the circulating fields for ~3 ms.
Work toward a squeezed light source for LIGO currently focuses on building an in-vacuum optical parametric oscillator to mitigate the influence of environmental disturbances; development of a ~10-m-scale filter cavity to generate frequency dependent squeezing; investigations of alignment and mode-matching techniques to enable robust long-term application of squeezing; and realization of low-loss polarization and detection optics. More speculative techniques are also being researched for application in future instruments.
Standard squeezing can improve high-frequency sensitivity useful for probing certain continuous-wave sources and the neutron star equation of state. Frequency dependent squeezing brings broadband improvements, which will increase the volume of the observable gravitational-wave universe by a factor of two with obvious benefits for all gravitational-wave searches.
Moreover, as quantum noise is the dominant noise source in LIGO, its reduction through squeezed light injection multiplies the effectiveness of all other possible upgrades. Reasonable predictions for a near-term upgrade to LIGO indicate that event rate can be increased by an order of magnitude in this way; a critical improvement at the dawn of gravitational-wave astronomy.
References
R.E. Slusher, L.W. Hollberg, B. Yurke, J.C. Mertz, and J. F. Valley, Phys. Rev. Lett. 55, 2409 (1985), Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity
Carlton M. Caves, Phys. Rev. D 23, 1693 (1981) Quantum-mechanical noise in an interferometer
H. J. Kimble, Yuri Levin, Andrey B. Matsko, Kip S. Thorne, and Sergey P. Vyatchanin, Phys. Rev. D 65, 022002 (2001), Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics
Roman Schnabel, Nergis Mavalvala, David E. McClelland and Ping K. Lam, Nature Communications 1, 121 (2010), Quantum metrology for gravitational wave astronomy
S. S. Y. Chua, B J. J. Slagmolen, D A Shaddock and D E McClelland, Class. Quantum Grav. 31 183001 (2014), Quantum squeezed light in gravitational-wave detectors
David E. McClelland, Nergis Mavalvala, Yanbei Chen, and Roman Schnabel, Laser Photonics Rev. 5, No. 5, 677–696 (2011), Advanced interferometry, quantum optics and optomechanics in gravitational wave detectors
The LIGO Scientific Collaboration, Nature Physics 7, 962–965 (2011), A gravitational wave observatory operating beyond the quantum shot-noise limit
J. Aasi et al., Nature Photonics 7, 613–619 (2013), Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light
John Miller, Lisa Barsotti, Salvatore Vitale, Peter Fritschel, Matthew Evans, and Daniel Sigg. Phys. Rev. D 91, 062005 (2015), Prospects for doubling the range of Advanced LIGO
Parametric Instabilities
Gravitational wave interferometric detectors are the most sensitive position meters in existence, aiming to measure strain (∆L/L) sensitivities of the order of 10-23. In order to achieve such incredible sensitivities, the LIGO detectors employ 4 km long Fabry-Perot cavities in the interferometer arms, storing nearly 1 MW of laser light when operating at full power. In this extreme environment, the optomechanical interaction between the optical field and the arm cavities' 40 kg optics leads to energy transfer from the arm cavity field to the mechanical mode of the interferometer optics in a runaway positive feedback process. In such processes, a carrier laser beam is scattered into an optical transverse mode by a vibrating mirror surface. The back action of transverse modes leads to energy being fed into the test mass causing an exponential growth of both mechanical and transverse mode amplitudes called Parametric Instabilities (PI).
Since the strengths of optomechanical interactions of interest are strongly dependent on stored optical power, parametric instabilities limit high power operation of gravitational wave detectors. Uncontrolled growth of transverse electromagnetic modes and mechanical mode amplitude causes malfunction of the detector due to the arm cavity lock loss.
Parametric Instabilities were recognized in 2001 and since then have been extensively studied. They were first observed at LIGO Livingston and have now been seen in both LIGO detectors.
In parallel to research on instabilities, a number of mitigation techniques, either passive or active, have been developed. In particular, solutions directly applicable LIGO involve active damping of acoustic modes by means of test mass electrostatic drive actuators, and thermal tuning of the optical modes using the test mass ring heaters.
Parametric Instability is strongly tuned by thermal changes in the radius of curvature of test masses, which occur due to thermal lensing. The mirror radius of curvature is not a fixed parameter, but a dynamic and tunable variable. Since this curvature directly tunes the instability gain, it is possible to find a solution to instabilities over the range of mirror radii of curvature within which the detector will operate. This method was successfully applied at both observatories, however, it is insufficient in the case of a small number of unstable modes.
We plan to implement an electrostatic actuator to control large numbers of unstable modes (predictions show ~40 modes at full power). This technique requires monitoring test mass mechanical modes and feeding corrected phase signals to the electrostatic drives located near the masses. The resulting reduction of the Q-factor of mechanical modes prevents instabilities.
We will also explore a novel method of passively controlling PI by reducing the Q-factor of the mechanical modes with a small resonant damper. The advantage of this method is that a vast number of modes can be controlled at once. The acoustic mode damper dissipates the strain energy of the test mass mode through a resistive element after converting it to electrical energy via the piezoelectric effect. A significant constraint on this technique is that it must preserve the inherently low mechanical loss of the test mass in the gravitational frequency band to maintain a low level of thermal noise. We’re currently working on designing the optimal acoustic mode damper with an ultralow thermal noise penalty.
While parametric instabilities remain a concern for high power operation, thanks to many years of theoretical and experimental work informed by direct observation, the challenges faced by gravitational wave detectors are now well understood.
Thermal Noise Experiment
Thermal fluctuations in mechanical systems (“thermal noise”) are a limiting noise source in current gravitational wave detectors, in the best frequency references, and in the field of macroscopic quantum measurement. The fact that thermal fluctuations can be limiting, despite having a magnitude typically of order 10-18 m, highlights the astounding precision at which these experiments operate.
Thermal noise in optical coatings has recently become a topic of great interest, as coatings have become the largest contributor to thermal noise in the above-listed areas of optical precision measurement. This fact can be understood simply by observing that while other parts of the mechanical system used in a gravitational wave detector or frequency reference cavity can be chosen to minimize thermal noise, the coatings must first satisfy strict requirements of optical properties. Those searching for new, high-reflectivity surfaces with low thermal noise are exploring wide-ranging possibilities; from new amorphous coatings produced with conventional ion beam sputtering techniques to crystal coatings and grating reflectors. Research in the area of coating thermal noise will allow us to extend the reach of next generation gravitational wave detectors, make ever more precise clocks, and probe more deeply the quantum nature of optomechanical interactions. To realize the full potential of gravitational wave observation, significant improvements in sensitivity will be needed beyond LIGO and other detectors currently under construction. Detector sensitivity is currently limited in the most astrophysically interesting frequency band by coating thermal noise.
Our research involves a novel method to measure optical coating thermal noise. At the heart of this method is a high-finesse optical cavity that resonates in three distinct fields: a horizontally polarized Gaussian TEM00 mode, and two vertically polarized Hermite-Gaussian modes, TEM02 and TEM20. The primary advantage of using multiple resonant fields in a high-finesses cavity is that all of these fields share the same sensitivity to changes in cavity length and laser frequency. On the other hand, each mode samples a different part of the coating and thus the coating thermal noise seen by each of the resonant modes is largely independent. Since this experiment measures the difference between the resonant frequencies of the TEM02 and TEM20 modes, all cavity length noises cancel, leaving only the desired coating thermal noise.
In addition to eliminating these noise sources, the unique folded cavity design of our experiment allows it to distinguish various sources of coating thermal noise and to characterize the properties of the coating materials involved. This complete coating thermal noise characterization leads to an understanding of the sources of thermal noise in a coating, and thus does much more to aid in the design of new coatings than a single coating thermal noise measurement.
Einstein 1905 versus Einstein 1915
In 1915, Einstein published his revolutionary theory of gravitation called The General Theory of Relativity. In this theory, Einstein rejected Newton’s theory that objects exert an instantaneous gravitational force on each other proportional to the product of their masses and inversely proportional to the square of the distance between them and which results in motions or accelerations of the masses involved. For example, in Newton’s theory, the planets and the sun exert forces upon each other that result in the planets following elliptical orbits about the sun. Newton’s theory had the “spooky” property that these forces were communicated everywhere in the universe instantaneously. In Einstein’s theory of gravitation, an object with mass warps spacetime, and other masses follow the shortest distance through this warped spacetime. Einstein’s theory had the happy property that this “gravitational information” was propagated at the speed of light. Moreover, Einstein’s showed that his theory could be shown to possess wavelike solutions that propagated through space also at the speed of light.
The purpose of the Advanced LIGO (aLIGO) detectors is to detect these gravitational waves and to use them to study the astrophysical objects that produce them rather like studying the stars by looking at the light they emit. In addition, a principle aim of the LIGO’s detectors is to confirm Einstein’s General Theory of Relativity.
The LIGO gravitational wave interferometers have been designed so that technical or non-fundamental sources of noise such as electronics or ground movement are much smaller than fundamental sources of noise such as those imposed by Quantum Mechanics or Statistical Mechanics. LIGO’s sensitivity to gravitational waves will be limited by the quantum nature of light at high frequencies between about 200 Hz and 10,000 Hz and by Brownian motion in the suspensions and test masses at frequencies from 10 Hz ~ 200 Hz. Ironically, in 1905, ten years before Einstein published his general theory of relativity he published two papers: one on the quantum nature of light and another on Brownian motion noise.
The quantum nature of light was first proposed by Einstein in his paper on the Photoelectric Effect in 1905. Here he quantized light energy to explain the how electrons are ejected from a metal when illuminated by light of different powers and wavelengths. This “quantization of light” means that light is detected in individual bundles of energy, subsequently called photons. One consequence of this quantization is that when using light to make a measurement it is necessary to account for the variation of the number of photons of light measured in a given interval of time, and that variation in photon number from interval to interval goes as the square root of the average number of photons measured per interval. Physicists call this Shot Noise; it limits LIGO’s sensitivity at frequencies above about 200 Hz. Einstein won his Nobel Prize in 1921 for his theory of the Photoelectric Effect.
Einstein’s Miracle Year also resulted in his papers on the Special Theory of Relativity, Mass-Energy Equivalence, and Brownian Motion. In 1827, Robert Brown, a botanist, observed how pollen grains suspended in a drop of water appeared to follow a random path. Brown’s observations were not explained for almost a century until Einstein developed his theory. In Einstein’s theory, a pollen particle (which is much larger than the molecules making up the fluid) is constantly buffeted by large numbers of molecules and slowly moves through the fluid in a random walk or diffuses through the fluid. Einstein found that the diffusion is a result of the viscosity of the fluid.
Viscosity can cause mechanical loss or dissipation. This is a process that can turn macroscopic motions into heat or microscopic motions. This connection between random motions and dissipation is now formalized in the Fluctuation-Dissipation theorem first formulated by Nyquist in 1928 and later proved mathematically by Callen and Welton in 1951. At frequencies below 200 Hz LIGO’s detector is limited by the Brownian motion noise of the coated test mass and the last stage of the suspension system. The dissipating element in these two cases is not the viscosity of a fluid but, in the case of the suspension, is the mechanical loss of the fused silica glass fibers suspending the mirror, and in the case of the mirror itself, it is the optical coating on the mirror substrate.
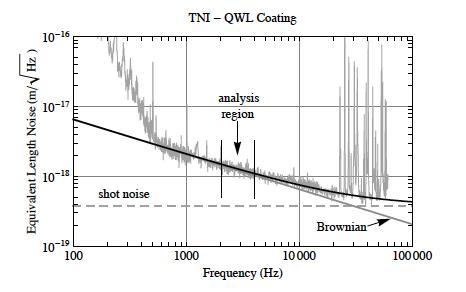
Since 2000, the LIGO Lab has been experimenting with measuring Brownian noise caused by coating mechanical dissipation. The first experiment carried out from 2000-2009, involved four suspended test-mass mirrors forming two Fabry-Perot interferometers and a single laser, and was called the Thermal Noise Interferometer (TNI). In this experiment, the suspended mirrors could be positioned using active feedback control, and both Fabry-Perot cavities were locked to the single laser frequency. The test masses were four inches in diameter and one inch thick and were separated by about two inches. The coating thermal noise measured on mirrors with advanced LIGO-like coatings is shown in the figure below.

LIGO Lab's Thermal Noise Interferometer. A large apparatus consisting of four suspended test-mass mirrors forming two Fabry-Perot interferometers and a single laser. (Caltech/MIT/LIGO Lab)
In these experiments, the Brownian motion was measured in the region between 500 Hz and 10 kHz (Villar 2010). However with four suspended test-mass mirrors, maintaining the alignment of the mirrors to the laser beams from day to day was prohibitive and thus made calibration of the experiment difficult. Moreover, the mirrors were suspended on single-loop wire suspensions that did not provide sufficient isolation at low frequencies from ground noise to allow measurements in the frequency band in which LIGO would be limited by coating Brownian thermal noise (30 Hz to 200 Hz).
The experiment was improved by adding a multiple pendulum suspension (current LIGO suspensions utilize a 4 stage suspension system) and an automatic alignment system (LIGO has both an optical lever system and a wavefront measurement system that uses the light in the interferometer for alignment). It was decided to follow an approach used at the National Institute of Standards and Technology in their laser frequency stabilization experiments and use two small mirrors rigidly bonded to precision polished glass spacers forming a Fabry-Perot arm cavity.
The coating thermal noise measured on mirrors with advanced LIGO-like coatings (Caltech/MIT/LIGO Lab)
We then mounted the two fixed spacer cavities in a common bracket with temperature control inside a single vacuum chamber. The new experimental setup used two lasers, each one independently frequency-stabilized to a cavity. The stabilized and spatially filtered light emerging from the two cavities was then combined with a beam splitter onto a photodiode and the resulting beat note (much like the beat note between two closely spaced guitar strings) signal was then spectrally analyzed to measure the noise imposed on the two laser beams by the cavity coating thermal noise. This scheme was easier to align and more stable throughout the day, and from day to day thus allowing more reproducible and reliable results. The results in the final figure below show that this new experiment produces Brownian coating noise measurements from 30 Hz to 800 Hz which encompasses the range of frequencies from 30 Hz to 200 Hz in which aLIGO is expected to be limited by coating Brownian noise (Chalermsongsak 2014).
References
Villar2010 - Akira E. Villar et al, “Measurement of thermal noise in multilayer coatings with optimized layer thickness,” Physical Review D 81, 122001 (2010).
Chalermsongsak2014 - Tara Chalermsongsak, “High Fidelity Probe and Mitigation of Mirror Thermal Fluctuations,” Dissertation, Caltech PMA, May 2014
Crackling Noise in Gravitational Wave Detectors
Xioayue Ni, Gabriele Vajente, Karin A. Dahmen, Julia Greer, Yuri Levin and Rana Adhikari
Introduction
Everyone has heard the crackling sound that occurs when you crumple a piece of paper (Houle1996). Over the past 25 years, we've come to understand that this crackling sound is an example of a universal phenomenon (Sethna2001) and is usually called crackling noise. When pushed slowly, many systems produce crackle noise in discrete events in a large range of sizes. Other examples of crackling include the slow rubbing of tectonic plates occasionally resulting in a large earthquake (Gutenberg1954), or the discrete step by step magnetization of a piece of iron in a slowly increasing magnetic field (Sethna1993). An experiment is underway in the LIGO Lab to look for crackling noise in the suspension systems used to isolate our test masses from seismic noise.
Gravitational Wave Detectors
All of the world’s large gravitational wave interferometers have shown unexplained noise at low frequencies between 10 Hz and 30 Hz. For some time, it has been suspected that crackling noise in the mirror suspensions might be at least partly to blame. Figure 1 below shows a diagram of LIGO’s quadruple pendulum suspension used to support the main test mass mirrors. The suspensions support the test masses vertically against the force of gravity while allowing almost unhindered motion along a line between the input and end test masses that define a detector arm. By unhindered we mean that at frequencies above about 10 Hz, the suspension elements, including wires, blades and glass fibers, only apply extremely small forces or torques that can disturb the mirrors.
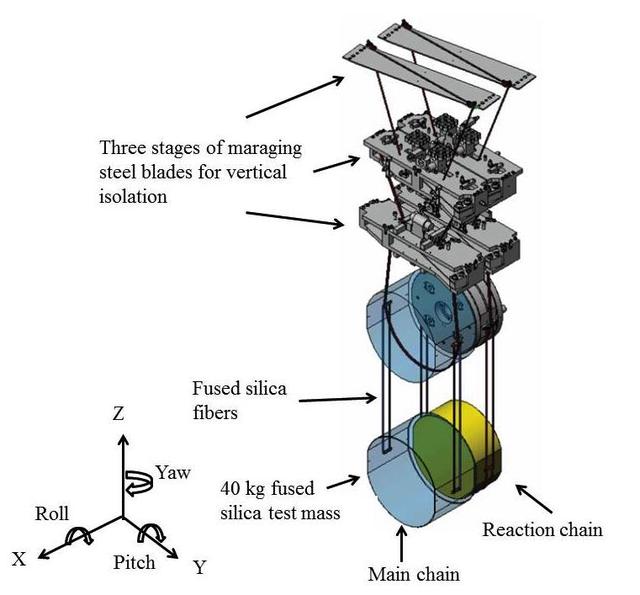
Figure 1. A drawing of the quadruple test mass suspension showing the 4 masses of the main chain and the 4 masses of the reaction chain (Caltech/MIT/LIGO Lab)
The potential crackling noise events we are searching for in our first Crackling Noise Experiment are impulsive releases of energy in the maraging steel blades, which provide vertical isolation in the aLIGO detectors.
First Crackling Experiment
Searching for crackling noise by detecting the motions of a suspended LIGO mirror would require a sensitivity as good as that of LIGO itself, which is not possible in a typical lab-scale (or "table top") experiment or on a typical tabletop experiment budget. Instead, we will look for the excess noise directly in a small cantilever blade and then extrapolate how this noise would be transferred to aLIGO test mass mirror (Levin 2012). A tabletop Michelson interferometer has been set up and operated in past years, trying to measure crackling noise in the form of non-linear up-conversion of low frequency (~100 mHz) motion of test maraging steel blades. This experiment was limited to 10-12 meters in a one second measurement time and we were unable to eliminate cracking noise as a possibility in the steel blades being used in LIGO, because of its limited sensitivity. Thus, we could not eliminate cracking noise as a possible problem for LIGO.
Second Crackling Experiment
Over the past year, we redesigned and built an upgrade of the first Crackling Experiment. This new experiment address the main issues affecting the first experiment’s sensitivity including, 1) seismic noise limited the first experiment so a double stage horizontal and vertical passive seismic isolation system was added, 2) laser intensity and frequency noise was improved by replacing the gas Helium-neon with a Nd:YAG 1064 nm laser similar to the master oscillator in LIGO, and increasing the laser power by a factor of 100 thus improving the interferometer sensitivity, 3) the main limitation of the first experiment was the clamping fixture used to attach test masses to the blades. In the new setup, the clamps are as close as possible to those used in LIGO, and the masses used to load the blades will be suspended with wires, thus virtually eliminating any coupling of blade tilts to the main interferometer mirrors.
The Second Crackling Experiment is designed to reach a sensitivity of 10-15 m (1/10 the diameter of a proton) in a one second measurement time. This will allow the detection of crackling noise in the steel blades at a level that will allow us to set an upper limit on its amplitude compatible with LIGO’s requirements.
Conclusion and Future
To date, we have not seen any noise in the LIGO measurement band resulting from crackling. In summer 2015 we will begin a series of experiments on several sets of steel blades. In the future we will begin studying other possible locations for the origin of crackling noise in the suspensions including: the KOH bonded silica ears on the mirrors, the glass suspension fibers in the last stage, the steel wire in the upper three pendulum stages, the welds of the glass fibers to the glass ears, and the break-offs of the wires from the cantilever blades.
References
Houle1996 - Paul A. Houle and James P., “Acoustic emission from crumpling paper”, Sethna, Physical Review E, Vol. 54, Number 1, July 1996, pp. 278- 283.
Sethna2001 - James P. Sethna, Karin A. Dahmen and Christopher R. Myers, “Crackling noise”, Nature, Vol 410, March 8, 2001, pp. 242-250
Gutenberg1954 - Gutenberg, B. & Richter, C. F., “Seismicity of the Earth and Associated Phenomena”, Princeton Univ. Press, 1954
Sethna1993 - Sethna, J. P. et al. “Hysteresis and hierarchies: dynamics of disorder-driven first-order phase transformations,” Phys. Rev. Lett. 70, 3347–3351 (1993).
Levin2012 – Yuri Levin, “Creep events and creep noise in gravitational-wave interferometers: Basic formalism and stationary limit,” Phys. Rev. D 86, 122004 – Published 19 December 2001