Two Black Holes Merge into One
Image Credit: SXS, the Simulating eXtreme Spacetimes (SXS) project (http://www.black-holes.org)
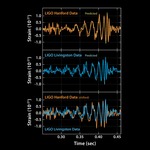
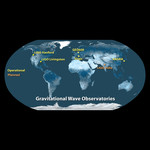
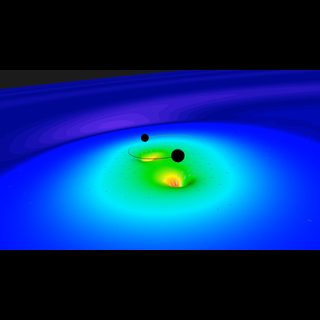
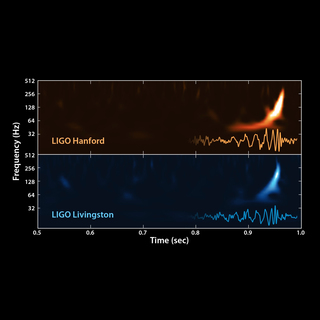
The collision of two black holes holes—a tremendously powerful event detected for the first time ever by the Laser Interferometer Gravitational-Wave Observatory, or LIGO—is seen in this still from a computer simulation. LIGO detected gravitational waves, or ripples in space and time generated as the black holes spiraled in toward each other, collided, and merged. This simulation shows how the merger would appear to our eyes if we could somehow travel in a spaceship for a closer look. It was created by solving equations from Albert Einstein's general theory of relativity using the LIGO data.
The two merging black holes are each roughly 30 times the mass of the sun, with one slightly larger than the other. The event took place 1.3 billion years ago.
The stars appear warped due to the incredibly strong gravity of the black holes. The black holes warp space and time, and this causes light from the stars to curve around the black holes in a process called gravitational lensing. The ring around the black holes, known as an Einstein ring, arises from the light of all the stars in a small region behind the holes, where gravitational lensing has smeared their images into a ring.
The gravitational waves themselves would not be seen by a human near the black holes and so do not show in this video, with one important exception. The gravitational waves that are traveling outward toward the small region behind the black holes disturb that region’s stellar images in the Einstein ring, causing them to slosh around, even long after the collision. The gravitational waves traveling in other directions cause weaker, and shorter-lived sloshing, everywhere outside the ring.
- JPG
- 150x150 (23.2 KB)
- 300x169 (24.8 KB)
- 600x338 (94.1 KB)
- 900x506 (212 KB)
- 1500x844 (562 KB)
- 3000x1688 (1.63 MB)
- 4800x2700 (3.51 MB)
- TIF
- Date
- February 11, 2016
- Location
- LIGO Lab
- ID
- ligo20160211d
- Type
- Simulation
- Credit
- The SXS (Simulating eXtreme Spacetimes) Project