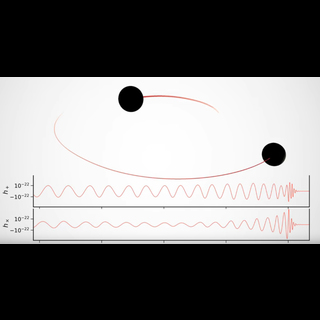
Artist's conception shows two merging black holes similar to those detected by LIGO on January 4th, 2017..
LIGO Catches its Third Gravitational Wave!
News Release • June 1, 2017
By Kimberly Burtnyk
[Click HERE to read the official LIGO Scientific Collaboration/LIGO Laboratory press release]
LIGO is thrilled to announce that it has nabbed its third gravitational wave in 18 months!
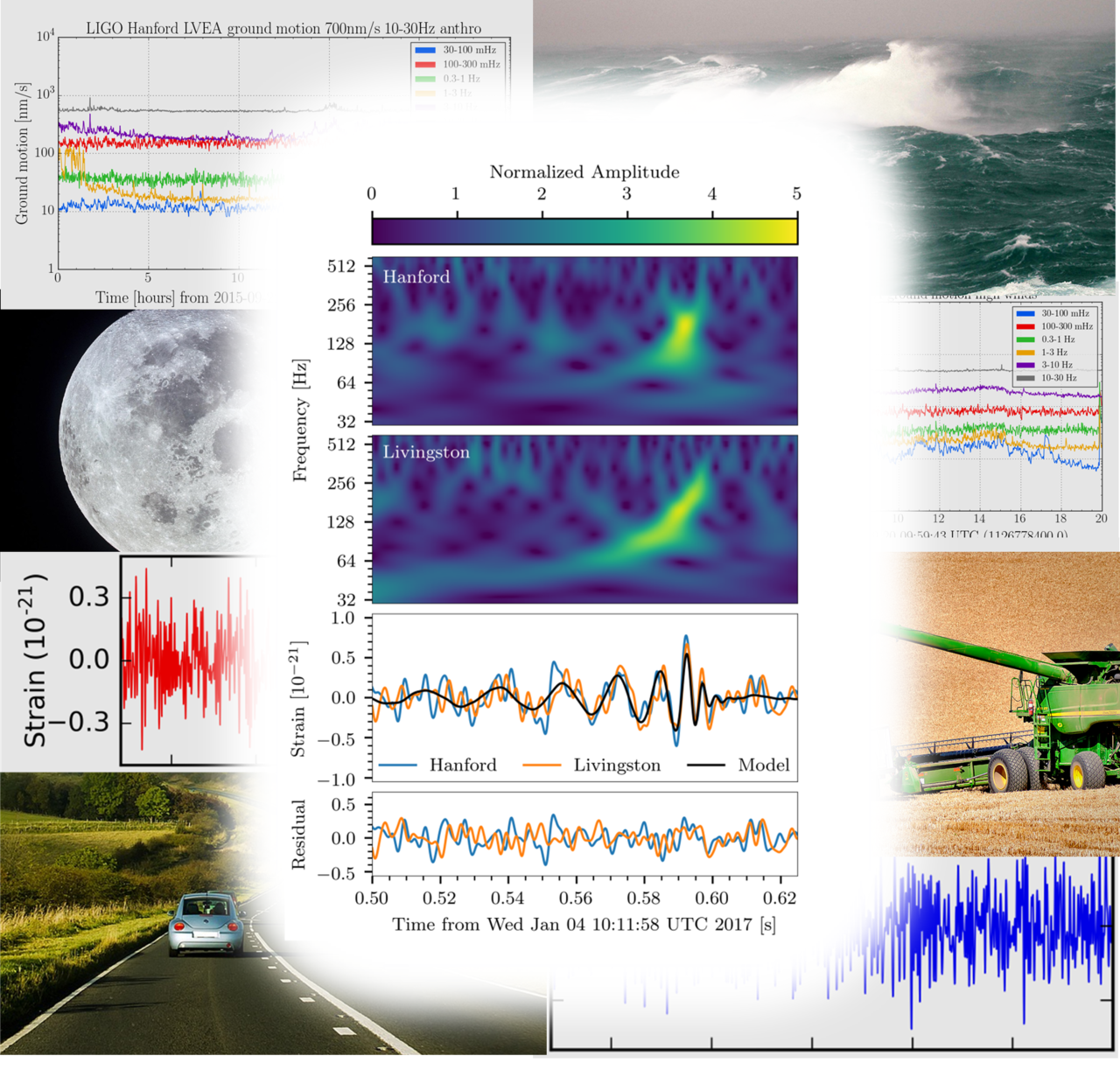
At 2:11:58 a.m. on January 4th 2017 the arms of LIGO’s Hanford, WA interferometer shivered. Three milliseconds later, Livingston’s interferometer followed suit. Even though parts of the U.S. were experiencing record cold temperatures, the trembling wasn’t caused by the frigid air of that winter morning. Rather, it was the shudder of space-time itself generated by the merger of two massive black holes in the distant universe: a gravitational wave had washed over the Earth, passing successively through the two detectors while most people in the U.S. were still asleep.
LIGO researchers quickly determined that the black holes were around 3 billion light years away from Earth when they collided, making this merger the farthest one yet observed (3 billion light years is about one-fifth of the way out to the ‘edge’ of the visible Universe). These waves had been traveling for around 3 billion years by the time they reached us.
Since learning of the detection, LIGO scientists have also determined that the two black holes involved in the merger were about 19 times and 32 times the mass of the Sun (with these masses, these objects add to a mysterious ‘new’ population of black holes with masses not known to astronomers prior to LIGO’s first detection). The resultant merged black hole is estimated to weigh about 49 times that of the Sun.
“But wait” you ask. “If you add 32 and 19, you get 51, not 49. What gives?”
On January 4th, 2017, LIGO detected two black holes merging into one. One of the black holes was 32 times the mass of the Sun (32 M⊙, where M denotes mass and ⊙ is a symbol for the Sun) while the other was 19 times the mass of the Sun. When they merged, they created a black hole 49 times the mass of the Sun. The coalescence instantly converted 2 solar masses of black hole mass into the energy that rattled spacetime enough to generate the gravitational waves we detected almost 3 billion years after it occurred. (Caltech/MIT/LIGO Lab)
The math isn’t wrong. When the black holes coalesced, 2 solar-masses worth of black-hole mass was converted into pure gravitational wave energy. Moreover, all that energy was released in the blink of an eye, a mere 0.12 seconds. At the moment of their collision, the black holes were orbiting each other at a velocity of six-tenths the speed of light!
Before they merged, the two black holes would have fit into spheres about 115 km (~70 mi.) and 190 km (~120 mi.) in diameter, respectively. The merged black hole would occupy a sphere about 280 km (~175 mi.) across. To put these numbers into perspective, consider this: Our Sun alone is 1.4 million km in diameter. Imagine compressing not just one, but 49 times the matter contained in the Sun into a sphere less than 200 km across.
Additional analysis of the data showed that this event also agreed (within the precision it can be measured) with predictions from general relativity, formulated by Albert Einstein over 100 years ago.
Despite the stupendous energy released by colliding black holes, detecting gravitational waves is excessively difficult since the effects they have on LIGO’s instruments are incomprehensibly small. This latest wave caused the spacetime occupied by LIGO’s arms to stretch and shrink by 0.000,000,000,000,000,001 (or 1×10-18) meters (a.k.a. an “attometer”). That’s 1000 times smaller than a proton!
Given how immeasurably small these effects are, how can we be certain this was a real detection of gravitational waves and not just a coincidental shudder at both observatories?
One of the first things we determined was whether or not the signal, which appeared nearly simultaneously at the Hanford and Livingston detectors, was just a fluke having nothing to do with gravitational waves from space. Looking more closely at the signal (e.g., at its shape and time of arrival at both detectors, and looking at how “noisy” the interferometers were at the time of the detection), LIGO researchers calculated that the chance that some random but nearly identical bits of ‘noise’ that happened to look like a gravitational waves appeared in both instruments at essentially the same time was 1 in 70,000 years. In other words, it is exceedingly unlikely that the signals detected in both interferometers were caused by chance noise bursts.
Teasing out a gravitational wave signal from LIGO data requires weeding through a lot of instrument and environmental noise. The image on top shows the result: the beautiful signature of our latest gravitational wave detection. (Caltech/MIT/LIGO Lab)
The other thing we do is to look to see if there were any ‘environmental’ events that could have made those signals. We look at lightning storms, power line fluctuations, radio signals, acoustic and seismic noise (e.g., trucks driving by, earthquakes), and many signals inside the instruments themselves to see if – by chance – we had nearly simultaneous external disturbances. None were found.
After crunching the numbers, LIGO scientists determined that they are 99.997% certain that the signal received was created in the distant Universe by the collision of two black holes. In other words, we can say with great certainty that LIGO has indeed observed a third pair of colliding black holes!
While LIGO continues to detect gravitational waves from merging black holes, electromagnetic (EM) observers are still hoping to spot a glimmer of light emanating from a gravitational wave event. To help make this happen, LIGO has partnered with 77 observatories around the world (including a couple in orbit), agreeing to let them know when we’ve detected a gravitational wave so they can look for some afterglow.
After this latest event, all 77 partners were alerted and 34 were able to search for some light. As with our previous two detections, nothing was seen, but that’s not surprising for two big reasons:
First, black holes are “black” because no light can escape them, even when they smash into each other, so we don’t expect to see light coming from the black holes themselves. You might then ask, “Why tell astronomers to look for something they can’t see?” While the black holes won’t give off light, if some ‘normal’ matter like leftover stellar matter from a supernova was caught up in the merger, a flash or afterglow of light might appear, and the remnants might shine for some time. Analyzing this light would yield incredibly valuable information about the event, especially (to a much higher degree of certainty) how far away the collision occurred. So with all can be gained from glimpsing some light from a merger, even if a flash of light or glow is unlikely, we will always tell our astronomy partners when we’ve detected gravitational waves, because you just never know.
Second, with only two detectors in our network, we aren’t yet able to tell astronomers precisely where to look, which makes finding an afterglow the ultimate needle in a haystack. In this latest detection, the area of sky that we determined could have contained the black holes was about 1200 square degrees. That’s the amount of sky that would be covered by 6000 full Moons. Since we don’t know how long any glow from a gravitational-wave generating event might last, searching all possible locations quickly is critical. But searching 1200 square degrees could take weeks, and the odds that an astronomer would search that just the right part of the sky containing the source of the waves are slim to none. But not for long.

This Mollweide projection/map shows the possible locations on the sky of the black holes that collided, generating the gravitational waves LIGO detected on January 4, 2017. The banana-shaped blobs cover 1200 square degrees, or about 3% of the sky (the entire sky covers about 41,000 square degrees). It would take 6000 full Moons to fill the search area. (Figure PRL citation)
How much space does 1200 square degrees cover? The large beige square represents 1200 square degrees. The full moon (small white circle) takes up about 0.2 square deg., and the blue square shows the search area LIGO could achieve if a third detector joined the search. (Caltech/MIT/LIGO Lab)
The situation will change dramatically when Virgo, LIGO's sister detector in Europe, comes back online later this year. With at least three interferometers detecting gravitational waves, we will be able to localize the source of the waves in a way similar to how three cellphone towers can narrow down the location of your phone. This will allow us to give our astronomy partners a much smaller piece of sky to search and greatly increase the odds that someone will spot an afterglow—if there is one to see. Even though we have yet to detect something that we expect to give off any light, the chance of being the first to detect a flash or residual glow associated with a gravitational-wave generating event keeps our astronomical partners interested in any alerts we send them. When that happens, LIGO will have demonstrated that it is a useful tool for gravitational-wave and electromagnetic astronomers alike.
For now, even without the ability to pinpoint the source, LIGO is certain that it has once again captured the last fraction of a second of the lives of two massive black holes as they merged into one, some 3-billion years ago. This latest detection bodes well for LIGO’s future and the future of gravitational wave astronomy as the observatory strives to further improve its sensitivity, and as more gravitational wave interferometers around the globe join the search.
GLOSSARY AND ADDITIONAL INFORMATION
Defining the ‘size’ of a black hole is a bit tricky because it’s not like black holes have well-defined edges. Nevertheless, astronomers can describe the “size” (i.e., spatial extent) of a black hole by measuring its sphere of influence on light. And that ‘sphere’ is defined by something called the Schwarzschild radius.
The Schwarzschild radius is the radius of a sphere such that, if all the mass of an object were to be compressed within that sphere, the escape velocity from the surface of the sphere would equal the speed of light. In other words, not even light could escape its gravity. That’s why black holes are called “black” holes. The size of the Schwarzschild radius is dependent on the mass of the object.
LIGO can determine the Schwarzschild radii of black holes by using information contained in the signals we receive from colliding black holes. While the signals do not reveal the ‘width’ of the black holes, they DO tell us how massive the black holes are. And mass is all you need to know to determine a black hole’s Schwarzschild radius.
There’s one more thing LIGO scientists need to take into account when determining the size of a black hole: whether or not the hole itself was spinning. Spinning black holes are harder to size up but in general, the faster the spin, the smaller its Schwarzschild radius.
Here’s a fun Schwarzschild radius calculator created by the University of Nebraska (Lincoln) that you can play with:
http://physics.unl.edu/~klee/flash_astro/bhole_sim010.swf
- Click “M⊙” (meaning, mass of the sun) from the pull-down menu and enter the number 1 in the box. This tells you how small a sphere you would have to pack all the mass of the Sun into if you wanted to make it a black hole. In other words, how big a "one solar-mass black hole" would be.
- Next, enter your weight in kilograms (choosing “kg” from the pulldown menu) to find out how small a "one you-mass black hole" would be!
At LIGO, the term ‘noise’ means any vibrations that are not caused by gravitational waves and that can ‘mask’ a gravitational-wave signal. Some of the sources of ‘noise’ we contend with include: a constant ‘hiss’ from photons arriving like raindrops at our light detectors; rumbles from seismic noise like earthquakes and the oceans pounding on the Earth’s crust; strong winds shaking the buildings enough to affect our detectors; scattered laser light taking the ‘wrong’ path through the interferometer; and many more subtle sources of background vibrations. All together, we call this ‘noise’.
It’s kind of like being in a crowded room during a boisterous party, and trying listen to someone with a very soft voice. You struggle to hear them above the noise: other people near and far are talking and laughing, the television is on with a sporting event replete with all the sounds associated with the stadium, glasses are clanking, bottles are opening, music is playing, people are coughing, sneezing, high-fiving, grabbing snacks from a crinkly bag or a glass bowl, someone else is trying to talk to you at the same time, cars are driving by outside, sirens are blaring in the distance, a helicopter flies overhead, dogs are barking etc. Imagine dealing with that situation 24/7. That’s the kind of chaos LIGO has to overcome to detect gravitational waves above the noise.
Electromagnetic (EM) Astronomer
Electromagnetic Observers use light, photons, or radio waves (different manifestations of the same thing really) to look at the sky. This is ‘traditional’ astronomy, which is now complemented by the completely separate ‘messenger’ of information – gravitational waves.
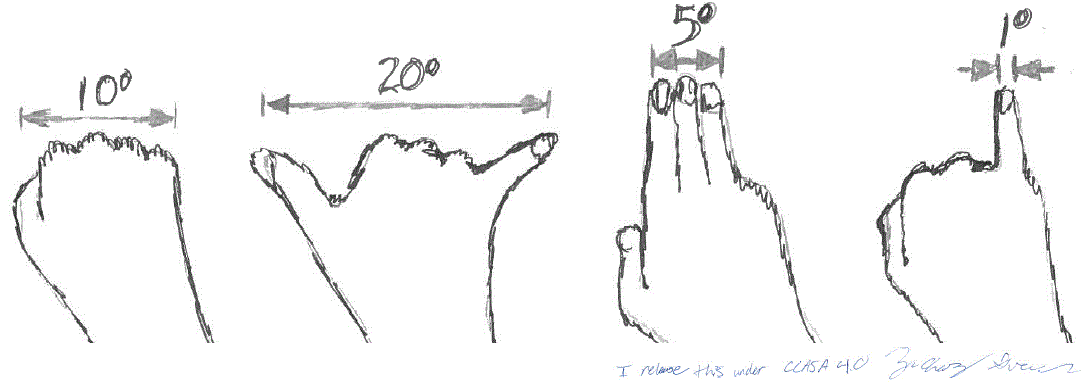
Astronomers use ‘square degrees’ to measure a patch of area on the sky. Just as degrees are used to measure parts of a circle, square degrees are used to measure parts of a sphere.
You can measure a degree on the sky by extending your arm and looking at the tip of your pinky finger. A degree on the sky is about the width of your pinky finger. So a ‘square’ degree is a patch of sky about one pinky-width high and one pinky-width wide. (Wiki CCASA 4.0 International)
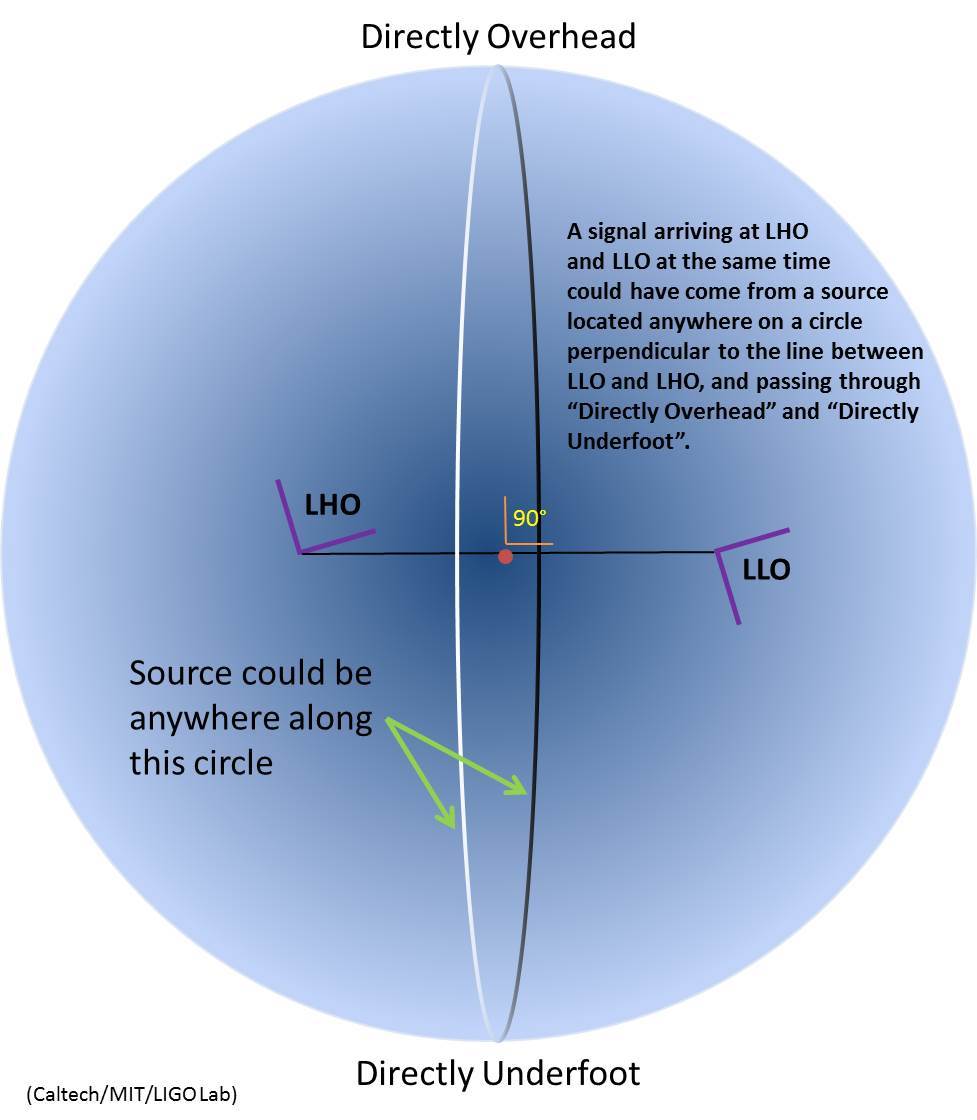
Individually, LIGO’s detectors can’t say much about where a source of gravitational waves lies in the sky. This is because they do not ‘point’ like a telescope; they pretty much look in all directions all the time.
With two detectors, and the fact that gravitational waves travel at the speed of light, we can look at the relative times of arrival of signals at the detectors to give us an idea of where the source might be on the sky. For example, if a source is exactly ‘overhead’ the signal will arrive at both detectors at the same time. But wait…the same timing would happen if the source was exactly ‘underfoot’. In fact, if a signal is received at both sites simultaneously, the source could be located anywhere along a perpendicular circle drawn directly between the two detectors and connecting overhead to underfoot (see figure at right)! While small differences in the detector’s sensitivity enable us to exclude some parts of the circle, that’s a very large search field.
On the other hand, if a source is along the line-of-sight between the two detectors it will arrive about 10 thousandths of a second (10 ms) earlier at the closer detector. If the timing is somewhere in between simultaneous and 10 ms, the circle of possible source location shifts in the sky accordingly.
Now….if you add another detector – Virgo – we will have vital additional information: we can say the source has to lie not only on the right circle between the two LIGO detectors, but also on circles connecting Virgo to each LIGO detector. There will be only one area on the sky where those three circles intersect, and this will give us a far better idea of where the signal came from.